Intro

A dynamic system can be studied in a constant manner, thanks to space-time.

So there is this troop of shy soldiers …

Who decided to form a line (row formation) as instructed by their commander. But they are too shy to face the commander, much less turning their ass to him, so they decided to either turn left or right. But hey, this way some of them are directly facing each other like this ><. Whenever such a thing happen, they immediately turn their back on each other (while blushing of course), like this <>, in exactly 1 second. The commander is amused and would like to know how long will it take before the troop stop moving around.

Despite the cringe-worthy problem statement

This turning-direction thing can be found very similar to here. Utilizing the approach used in that solution, one can abstract the transition from “><” to “<>” as the two “>” and “<” moving through each other simultaneously (“>” to the right 1 step and “<” to the left 1 step). So the process of achieving equilibrium can be described as the two sets “>”s and “<”s polarizing to the right and to the left respectively. The final result will look something like this ”< < < ….< < > >…> > >”.

And again, we simplify the problem by ignoring the “<” signs, thanks to the fact that once the “>”s are polarized, so are the “<”s. The process is then described as starting from ”- - - > - > > - - > -“ and reach ”- - - - - - > > > > > > >” in the end.

Now observe the movements of “>”s, there is only two situations:

If there is a blank immediately ahead, any “>” will occupy the blank in 1 sec.
If there is a “>” immediately ahead, the “>” will do nothing.

That is as far as I can go in abstracting the problem. And although things seem much less messy now than it is originally, the dynamic system is still somewhat chaotic and hard to handle. So now it is time to be inspired by the space-time idea.

A constant model

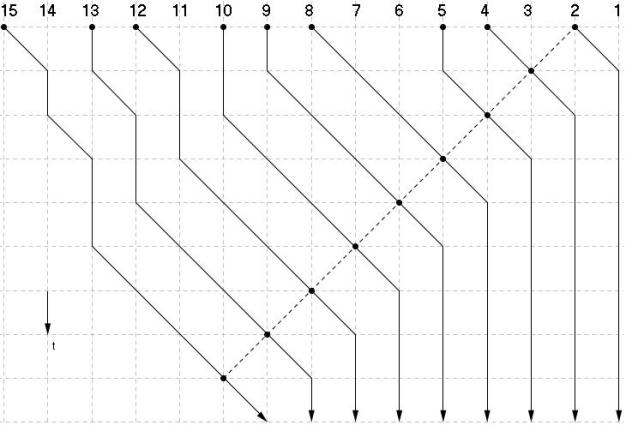
The image illustrates the situation where our “>” start at positions 15, 13, 12, 10, 9, 8, 5, 4, 2. It models the traces each “>” makes in space time, since the movements are made in 1D-space, its corresponding space-time is 2D. Now we go on observe some of the properties displayed in this model.

At the end of every trace, there is a vertical line expanding itself to the infinity of time, that is indeed when the corresponding “>” reaches its destination. Let’s exclude these obvious trace segments, any other segments that are vertical signifies the time where their corresponding “>” wainting for a free spot to move on. Let’s call these segments struggling.
The sloping segments indicates that their corresponding “>” are moving forward frely. Let’s call these segments free.
Any pair of traces are non-intersecting.

Although I’m so tempted to call the traces world lines, I assumed not being enough of a string-theory enthusiast to use the term. Nevermind, let’s move on doing some obvious things before cracking the problem.

Consider the extreme case

That is when there is absolutely no blank slot for anyone to move on. Sketch this situation and any one realize that, even though the struggleness is maximum, there is still no struggling segment after each trace reaches a limit point. Such limit points lie on a line, which is the dotted one in the illustration above: a sloped dotted line starting from the first “>”’s initial position. This line is realized naturally from this extreme case and is itself quite self-explanatory, so I’ll leave it there.

After this limit point, every trace follow the same pattern: freely move to the designated destination and then extends vertically infinitely.

What does all this leads to?

We can infer the answer directly from the limit point of the last “>”. The operation is quite trivial using geometry, so I’ll leave it at that and proceed to solve the problem of finding this particular limit point.

It is obvious that the limit point of this last “>” must be below the limit point of the second last. Thus it depends on the limit point of the second last, and similarly that limit point depends on the third last’s. So a reasonable thing to do is to consecutively define the limit points starting from the first one, all the way to the last.

How the limit points define their nexts

Limit points are define on the basis of their respective traces. Consider the trace of a particular “>”, the best it can do is to freely move until it reaches the limit line at the limit point. But if this limit point ends up being somewhere no lower than the previous limit point, we are violating some rules here. Namely, the all-free trace is too free.

It must struggle a little, just a bit enough to end up right besides (and below) the previous one. And in fact, the two cases above (all-free and struggle-just-enough) are sufficient to describe all traces.

The work is done, what left is a bit of coding

Solution (self-explanatory)

count := 0;
for i:=1 to N do if A[N-i+1] = '>' then begin
  inc(count);
  if count = 1 then begin
    mid := 2 * i;
    first := i;
  end else
    if (first + i) < mid + 2 
      then mid := mid + 2 {all free}
    else mid := first + i {struggle enough}
end;

solution := mid - first - count;