Intro

Keep calm and see through the clutter. Maths is meant to be simple.

So there is this messy problem I’ve encountered

Let’s \( \Delta ABC \) inscribes circle \( (O) \). \( D \in BC \) such that \( AD \) divides \( \widehat{BAC} \) equally. P is an arbitrary point on segment \( AD \). Let \(E, F\) be the intersections of \(BP\) with \(AC\), and \(CP\) with \(AB\) respectively. Through \(P\) draw a line perpendicular to \(BC\), this line intersects with \(EF\) at \(N\) and \(BC\) at \(M\). Let \(L\) be the intersection between \(OP\) and \(AN\). Prove that \(ML\) always go through a fixed point as \(P\) slides on \(AD\).

Too many intersections huh? It is not until now that I started to realize people need to stop giving problems like those. But again, simple and beautiful ones are rare. So kids like me back then have no other way but to train our mind to be calm and collected while coping with such problems. Let’s see how to deal with this mess.

A glance at our battle

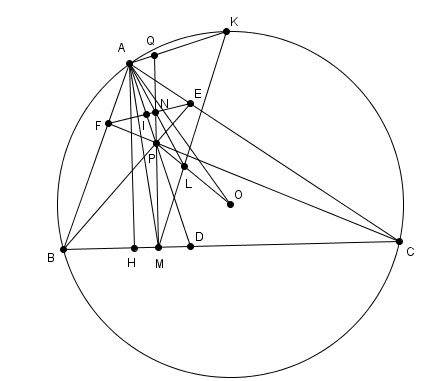
The problem with intersection

Forget the problem for a moment. Let \(Z\) be the intersection between any two segments \(XY\) and \(VT\). It is clear that the less we know about \(X, Y, V, T\) (what are their properties? positions? relations with each other and with the context?) the more confused we are about \(Z\). In fact, My conjecture is that if \(f(.)\) is a measure of how clueless we are about something. then

\[f(Z) = f(X)f(Y)f(V)f(T)\]

And yet in the original problem, we have too many of them, recursively in fact. What to do? It is often the answer is to look at our battle in a new light, such that variables vanished and the mess becomes more revealing. Sweet, let’s go through the solution shall we?

Forget about \(L\)

\(L\) is the last thing to be defined in the problem. Talking in \(f()\) fashion, it is an exponentially confusing point. And we have to deal with this variable directly as it also appears in the question. But how about throwing it away? How about that fixed point that \(ML\) always pass through? How can we use it to introduce some more stability?

Every post-beginner highschool maths student know what is the answer to this problem after some few sketches with different values of \(P\). In this case \(K\), the midpoint of arc \(BAC\) of \((O)\) is the answer. Knowing this, the trick is to prove \(MK\), \(AN\) and \(OP\) converges and we have successfully eliminated \(L\) from the equation.

We are now left with \(M, K, A, N, O, P\). In which \(O, A, P\) are the basis of the problem, \(M, N\) are on the next level, and \(K\) is there for the absence of \(L\).

Which amongst these 6 can be thrown away?

As in the previous part, the way we hide variables depends on how we re-state our question. How to prove these three line segments converge? Look at them, really soon one should realize that there is an interesting thing that not any “three-converging-lines” problems have: \(MP\) and \(OK\) is parallel.

How do we use this fact? There is very nice things about two line segments being parallel that someone who is familiar with geometry can sense in the air: equal angles, congruent triangles, equal ratios and a huge knowledge base developed around such situation. There is so much to be used, but what is the key to this “converging-line” problem?

You may have your own idea, but my pick is to re-phrase our question to proving that \(AN\) divides \(OP\) in the ratio \(MP:OK\), or \( MP:R \), which naturally leads to the convergence. And hey, there is now the constant \(R\) in our question statement, what a pleasant thing to have isn’t it :)

We can now officially forget about \(K\)!

Be careful not to introduce new variable

Talk about \(AN\) dividing \(OP\), one should never bring \(L\) back to the equation because we tried hard forgetting about it in the beginning. So, the walk around is to use trigonometry to talk ratios instead. Let the ratio obtained from this division be \(r\)

\[r = \frac{AP sin NAP}{R sin NAO}\]

Remember that in the end, we need

\[r = \frac{MP}{R}\]

Bridging the above two equations gives (\(R\) is cancelled!)

\[\frac{sinNAP}{sinNAO} = \frac{sin PAM}{sin MAH}\]

One thing we know about these angles: \(AD\) is the bisector of \(\widehat{OAH}\), So the solution is finalised if \(AD\) is also the bisector of \(\widehat{MAN}\). Before going any further, let’s step back and look at how far we’ve got: now the question in mind involves only \(A, D, M\) and \(N\), how simple!:) This is very likely a practice problem in some textbook and thus, should have multiple solutions ;)

For the sake of completeness, I’ll go for one but don’t limit yourself to it!

Let’s prove a more general problem!

Knowing that \(AK\) and \(AD\) are perpendicular, it is sufficient to prove that \(Q,P,N,M\) are harmonic (the bisector comes accordingly). How?

Sure this must be derived from the fact that \(A,P,I,D\) are harmonic. So, the question to ask is whether \(AQ\), \(IN\) and \(MD\) converge? Notice these lines are actually \(AK\), \(EF\) and \(BC\), and these are known to converge. All because \(AD\) divides angle \(A\) of the triangle equally.

We didn’t even use the fact that \(MP\) is perpendicular to \(BC\), so the problem we solve is more general than the original.